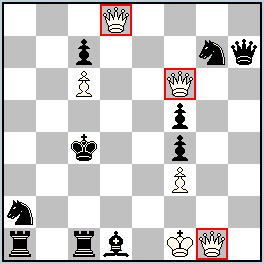
Enlevez, s’il vous plaît, le Pion blanc f3, rajoutez un Caméléon-Cavalier blanc d4 et regardez ces trois couples de coups :
          I) Rd3 CAb3(=F)+
          II) Rç5 CAé2(=F)+
          III) Rç3 CAé6(=F)+
Dans I), é4 n’est pas gardé, pas plus que ne le serait ç3 sans le CAf6 ; 1.Tç3 CAfd4(=C) résout a) avec le Pion blanc f3.
Dans II), b4 n’est pas gardé, pas plus que ne le serait d5 sans le CAd8 ; 1.Cb4 CAdd4(=C) résout b) avec le Pion blanc é4.
Dans III), ni b4 ni ç2 ne sont pas gardés et le CAg1 est superflu ; 1.Tç2 CAgd4(=C) résout c) avec le Pion blanc a3.
Les Caméléons construisent des batteries en s’interceptant cycliquement les uns les autres, à savoir f6 avec d8, d8 avec g1, g1 avec f6 : une idée formidable ! Le danger d’une trop grande symétrie entre b) et c) avec la quatrième traverse comme axe est évité de main de maître ; les fuites d5 et ç2 sont asymétriques et b4 est une fois bloqué, une fois gardé. Par ailleurs ç2 est bloqué mais ç6 gardé (f6 et g1 sont postés asymétriquement !), tandis que d3 et d5 sont gardés asymétriquement par le CAd8 (avec le Pion a3) contre le Pion é4 (le CAd8 disparaît !). Le jumelage est suffisamment subtil, la position pas trop encombrée. En comparaison des autres prix, ce problème n’est pas aussi élégant, mais bien plus sophistiqué. (Juge : Jörg Kuhlmann)

a) 1.Tç3 CAfd4(=C) 2.Rd3 CAb3(=F)#
b) 1.Cb4 CAdd4(=C) 2.Rç5 CAé2(=F)#
c) 1.Tç2 CAgd4(=C) 2.Rç3 CAé6(=F)#